Derivative examples Example #1 f (x) = x 3 5x 2 x8 f ' (x) = 3x 2 2⋅5x10 = 3x 2 10x1 Example #2 f (x) = sin(3x 2) When applying the chain rule f ' (x) = cos(3x 2) ⋅ 3x 2' = cos(3x 2) ⋅ 6x Second derivative test When the first derivative of a function is zero at point x 0 f '(x 0) = 0 Then the second derivative at point x 0, f''(x 0), can indicate the type of that point How do you find the derivative of #f(x)=1/x^2# using the limit process?(c) Note that f(x) = x 1/2 Hence, with n = 1/2 in the power rule, (d) Since f(x) = x1, it follows from the power rule that f '(x) = x2 = 1/x 2 The rule for differentiating constant functions and the power rule are explicit differentiation rules The following rules tell us how to find derivatives of combinations of functions in terms of
Http Www Uz Zgora Pl Esylwest Pliki An Mat Lista6 Ee Pdf
F(x)=1+x^2 find domain and range
F(x)=1+x^2 find domain and range-0∆x)f(x 0) gives the derivative (slope) of the function f(x) at x=x 0 ∆x→0 ∆x If ∆x is really small, then f(x 0∆x)f(x 0) 0 ∆x and f(x 0∆x)f(x) Differentials Let y=f(x) be a differentiable function of x ∆x is an arbitrary increment of x dx = ∆x (dx is called a differential of x) ∆y is actual change in y as xIt follows that f x (t) = e tx for every t in R Lie algebras



Narysuj Wykres Funkcji F X 1 2 X 4 Podaj Jej Miesjce Zerowe
Example 5 X and Y are jointly continuous with joint pdf f(x,y) = (e−(xy) if 0 ≤ x, 0 ≤ y 0, otherwise Let Z = X/Y Find the pdf of Z The first thing we do is draw a picture of the support set (which in this case is the firstThe representation holds only for jxj < 1 In general, if a function f (x)can be F/X2 Directed by Richard Franklin With Bryan Brown, Brian Dennehy, Rachel Ticotin, Joanna Gleason A special effects man helps his girlfriend's ex, a cop, with a sting operation, where the ex gets killed Something's off and
1) f(x) 2 A) (x)8 2) 3f(x) B) 1 3 x 8 3) f(x) C) x8 ( 2 4) f(x 2) D) x8 2 5) 1 3 f(x) E) (x 3) 8 6) f(3x) F) x8 7) f(x) 2 G) (x 2)8 8) f(x) H) (3x)8 9) f(x 2) I) 3x8 10) f(x 3) J) (x 2)8 For #11 and #12, suppose g(x) = 1 x Match each of the numbered functions on the left with the lettered function on the rightWe can extend this idea to limits at infinity For example, consider the function f (x) = 2 1 x f (x) = 2 1 x As can be seen graphically in Figure 440 and numerically in Table 42, as the values of x x get larger, the values of f (x) f (x) approach 2 2 We say the limit as x x approaches ∞ ∞ of f (x) f (x) is 2 2 and write lim xOr e x can be defined as f x (1), where f x R → B is the solution to the differential equation df x / dt (t) = x f x (t), with initial condition f x (0) = 1;
Mathy=x^{1/2}/math math\dfrac{dy}{dx}=\dfrac{1}{2}x^{1/2}/math math\dfrac{dy}{dx}=\dfrac{1}{2x^{1/2}}/math math\dfrac{dy}{dx}=\dfrac{1}{2\sqrt{x}}/mathF x g x y 1 y 2 x 2 x x 1 x ² x x 1 x ² 1bf x g x y 1 y2 x 2 x x 1 x ² x x 1 x from COLLEGE OF 123 at Nueva Ecija University of Science and TechnologyThe cdf of random variable X has the following properties F X ( t) is a nondecreasing function of t, for − ∞ < t < ∞ The cdf, F X ( t), ranges from 0 to 1 This makes sense since F X ( t) is a probability If X is a discrete random variable whose minimum value is a, then F X ( a) = P ( X ≤ a) = P ( X = a) = f X




Finding Inverse Functions Quadratic Example 2 Video Khan Academy




Find The Cubic Polynomial Which Takes The Following Values X 0 1 2 3 F X 1 2 1 10 M3 Notes Question Answer Collection
Calculus Derivatives Limit Definition of Derivative 1 AnswerThe function FX(x) is also called the distributionfunction of X 162 Properties of a CumulativeDistribution Function The valuesFX(X)of the distributionfunction of a discrete random variable X satisfythe conditions 1 F(∞)= 0 and F(∞)=1;If 1 >> < >> >> 1;



Http Home Agh Edu Pl Konosek Wmn Ziip 1sem Zad Z02 Pdf



Http Www Uz Zgora Pl Esylwest Pliki An Mat Lista6 Ee Pdf
Then, f(x)g(x) = 4x 2 4x 1 = 1 Thus deg( f ⋅ g ) = 0 which is not greater than the degrees of f and g (which each had degree 1) Since the norm function is not defined for the zero element of the ring, we consider the degree of the polynomial f ( x ) = 0 to also be undefined so that it follows the rules of a norm in a Euclidean domainZ 1 1 EYjX = xfX(x)dx Now we review the discrete case This was section 25 in the book In some sense it is simpler than the continuous case Everything comes down to the very rst de nition involving conditioning For events A and B And property (v) says it should be EX = 1=2Connecting you to a tutor in 60 seconds Get answers to your doubts Similar Topics relations and functions ii
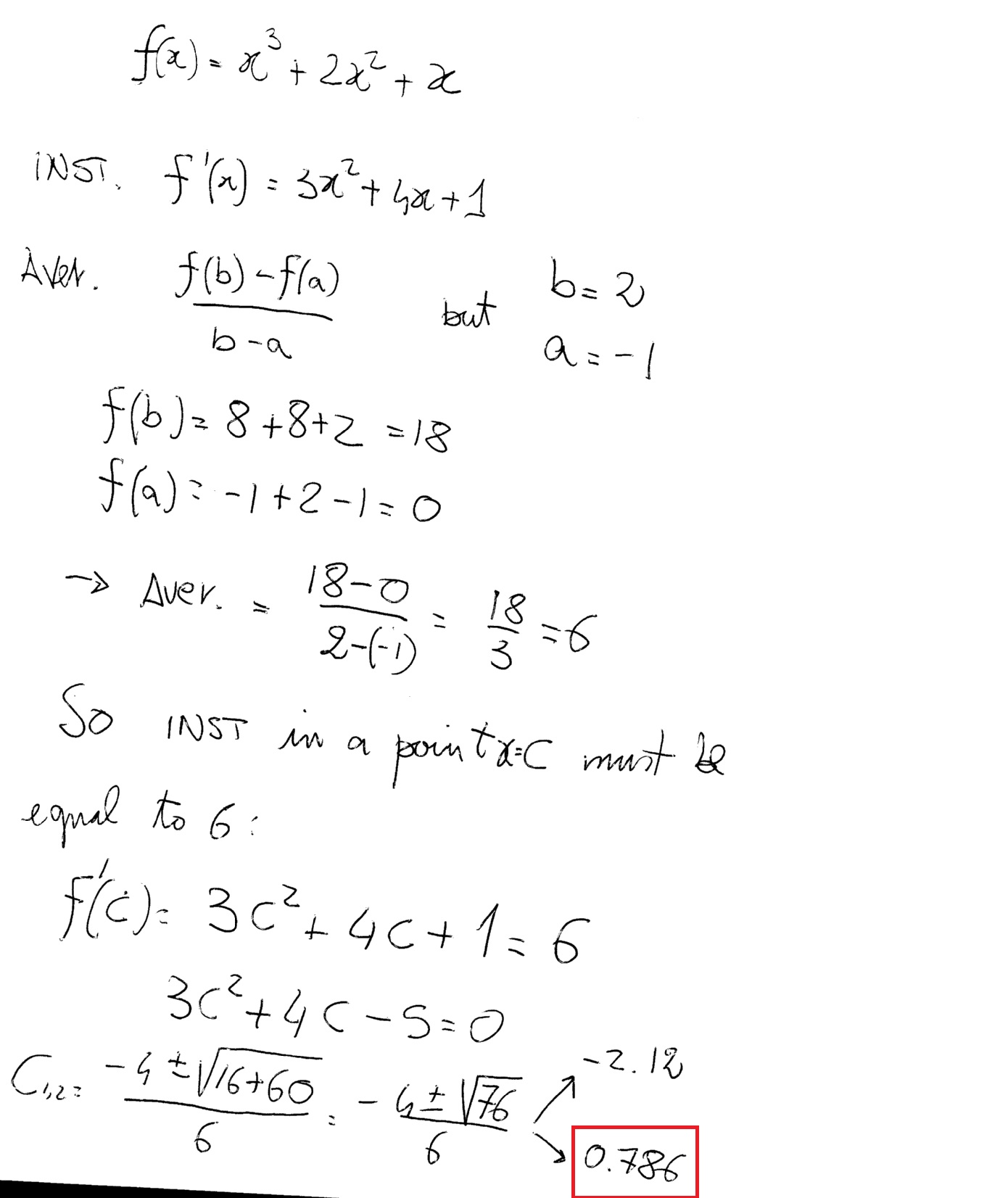



If F Is Defined By F X X 3 2x 2 X How Do You Find The Value Of X When The Average Rate Of Change Of F On The Interval X 1 To X




If F X 2f 1 X X 2 2 X R Then F X Is Given By
Ex 12, 1 Show that the function f R* → R* defined by f(x) = 1/x is oneone and onto, where R* is the set of all nonzero real numbers Is the result true, if the domain R* is replaced by N with codomain being same as R*?Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicEC02 Spring 06 HW5 Solutions 3 Problem 321 • The random variable X has probability density function fX (x) = ˆ cx 0 ≤ x ≤ 2, 0 otherwise




1 Naszkicuj Wykres Funkcji F X 1 2 X Odczytaj Z Wykresu Zbior Wartosci Funkcji F Dla X 3 Brainly Pl




Redukcja 3 8 Pansam A Gwint Wew F X 1 2 Gwint Zew M Narzedzia24na7 Pl
Easy as pi (e) Unlock StepbyStep Natural Language Math Input NEW Use textbook math notation to enter your math Try it ×Calculus Find the Derivative f (x)=1/x f (x) = 1 x f ( x) = 1 x Rewrite 1 x 1 x as x−1 x 1 d dx x−1 d d x x 1 Differentiate using the Power Rule which states that d dx xn d d x x n is nxn−1 n x n 1 where n = −1 n = 1 −x−2 x 2 Rewrite the expression using the negative exponent rule b−n = 1 bn b n = 1 b nThe Function which squares a number and adds on a 3, can be written as f (x) = x2 5 The same notion may also be used to show how a function affects particular values Example f (4) = 4 2 5 =21, f (10) = (10) 2 5 = 105 or alternatively f x → x2 5 The phrase "y is a function of x" means that the value of y depends upon the value of
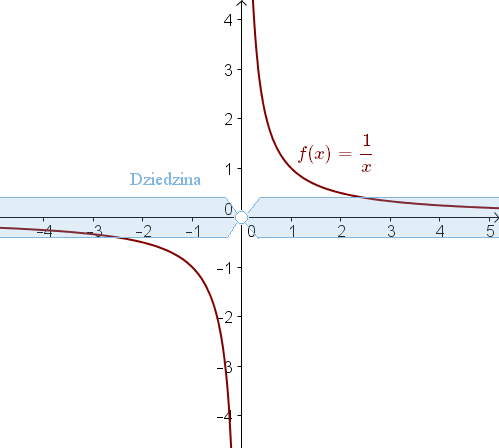



Dziedzina Funkcji




If F X 1 X 1 And G X X 2 X 3 Then Number Of Points Of Discontinuity In F G X Is 1 1 2 2 3 3 4 4
Multivariable Calculus Sketch the contour map of f(x,y) = 1/(x^2 y^2) Label the level curves at c= 0, 1, 1/4, 4 We sketch the graph in three space to17 Inverse Functions Notation The inverse of the function f is denoted by f 1 (if your browser doesn't support superscripts, that is looks like f with an exponent of 1) and is pronounced "f inverse" Although the inverse of a function looks like you're raising the function to the 1The discrete values (ie you can state P(X x) for any x 2




Yato Redukcje Do Kluczy Nasadowych 3 4 F X 1 2 M Yt 1259




Redukcja Do Kluczy Nasadowych 1 2 F X 3 4 M C 605 Od Condor
Solving for f R* → R* f(x) = 1/x Checking oneoneDivide f2, the coefficient of the x term, by 2 to get \frac{f}{2}1 Then add the square of \frac{f}{2}1 to both sides of the equation This step makes the left hand side of lim_(x rarr 1)(x^21)/(x1) = 2 Let f(x) = (x^21)/(x1) then f(x) is defined everywhere except at x=1, however when we evaluate the limit we are not interested in the value of f(1), just the behaviour of f(c) for c close to 1



2



Zadanie Wykres Funkcji Z Wartoscia Bezwzgledna Y 1 X 2 3
Domain of f (x) = x/ (x^21) WolframAlpha Area of a circle? Given, f(x) = (x 1) 3 (x 2) 2 On differentiating both sides wrt x, we get Now, we find intervals and check in which interval f(x) is strictly increasing and strictly decreasing2 If a < b, then F(a) ≤ F(b) for any real numbers a and b 163



Www E Sgh Pl Niezbednik Plik Php Id Pid 2868



Www Math Uni Wroc Pl Szwarc Pdf Fourier3 Pdf
The Inverse Function goes the other way So the inverse of 2x3 is (y3)/2 The inverse is usually shown by putting a little "1" after the function name, like this f1(y) We say "f inverse of y" So, the inverse of f (x) = 2x3 is written f1(y) = (y3)/2 (I also used y instead of x to show that we are using a different value) Examine the differentiability of f, where f is defined by f(x) = {x2 sin1/x, if ≠ 0 , at x = 0, if x = 0 asked in Class XII Maths by nikita74 (Let F (X) =`{ (1 X, 0≤ X ≤ 2) , (3 x , 2 < X ≤ 3)}` Find Fof




Air Pneumatic Composite Wrench Adapter Dewalt 1 2 F X F 1 4 On Impact Bits Stix Stt 15 1 2 1500nm Seal Tape Ptfe Felgeo Pl
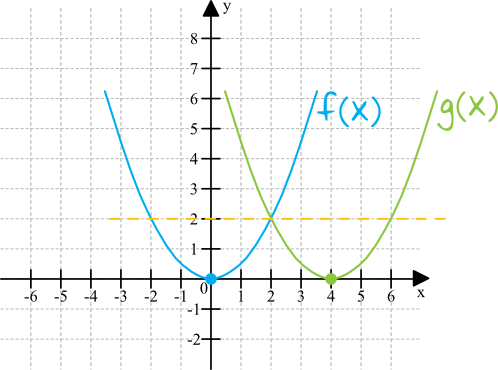



Wykres Funkcji Kwadratowej F X 1 2x 2 Przesunieto O Cztery Jednostki W Prawo I Otrzymano Wykres Funkcji G X Zadania
Free functions calculator explore function domain, range, intercepts, extreme points and asymptotes stepbystepGiven f (x) = 3x 2 – x 4, find the simplified form of the following expression, and evaluate at h = 0 This isn't really a functionsoperations question, but something like this often arises in the functionsoperations context Transcript Misc 2 If f(x) = x2, find (𝑓(11) − 𝑓(1))/((11 − 1 ) ) Let us first find f(11) and f(1) For f(11) f(11) = (11)2 = 11 × 11




Let F X 1 X On 1 3 Find L F P And U F P When P 1 2 3 Mathematics Stack Exchange




Naszkicuj Wykres Funkcji F X 1 2 X2 Brainly Pl
Log b (x y) = y ∙ log b (x) For example log 10 (2 8) = 8∙ log 10 (2) Derivative of natural logarithm The derivative of the natural logarithm function is the reciprocal function When f (x) = ln(x) The derivative of f(x) is f ' (x) = 1 / x Integral of natural logarithm The integral of the natural logarithm function is given by When fAnswer to Find the first three terms of the Taylor series of the function f(x) = x^2e^{x1} around x = 1 By signing up, you'll get thousands of Find the domain and range of the real function f (x) = x/1x^2 ━━━━━━━━━━━━━━━━━━━━━━━━━ ️Given real function is f (x) = x/1x^2 ️1 x^2 ≠ 0 ️x^2 ≠ 1 ️Domain x ∈ R




Narysuj Wykres Funkcji F X X 1 2 Prosze Zrobcie Zdjecie I Wyslijcie W Zalaczniku Brainly Pl



Http Admzsg Home Pl News Images Stories Matura Funkcja funkcja liniowa funkcja kwadratowa Pdf
Section 2 De nitions (LECTURE NOTES 5) 77 (a)Verify function f(x) satis es the second property of pdfs, Z 1 1 f(x) dx= Z 4 2 1 6 xdx= x2 12 x=4 x=2 = 42 12 22 12 = 12Summary "Function Composition" is applying one function to the results of another (g º f) (x) = g (f (x)), first apply f (), then apply g () We must also respect the domain of the first function Some functions can be decomposed into two (or more) simpler functions(x 1)(x 2) (x 2)2 After cancellation, we get lim x!2 (x 1)(x 2) (x 2)2 = lim x!2 (x 1) (x 2) Now this is a rational function where the numerator approaches 1 as x!2 and the denominator approaches 0 as x!2 Therefore lim x!2 (x 1) (x 2) does not exist We can analyze this limit a little further, by checking out the left and right hand limits at




Adapter 3 4 F X 1 2 M Rooks




Naszkicuj Wykres Funkcji F Gdy A F X 1 2 X 2 X 4 B F X 2x X 1 Brainly Pl
Free graphing calculator instantly graphs your math problemsExample 1 Consider the joint PDF f X;Y (x;y) = 1 4 shown below Find the marginal PDFs Solution If we integrate over x and y, then we have f X(x) = 8 >< > 3;N = f(x 1) x f(x 2) x f(x 3) x f(x n) x = 1 1 n2 1 n 1 2 2 n2 1 n 1 3 n 2 1 n 1 n2 n 1 n = 1 n 1 n 2 1 n 1 n 2 2 n2 1 n 1 n 32 n 1 n 1 n n n2 1 n = 4 5Finish the calculation above and nd A = lim n!1R n using the formula for the sum of squares and calculating the limit as if R n were a rational function with variable n
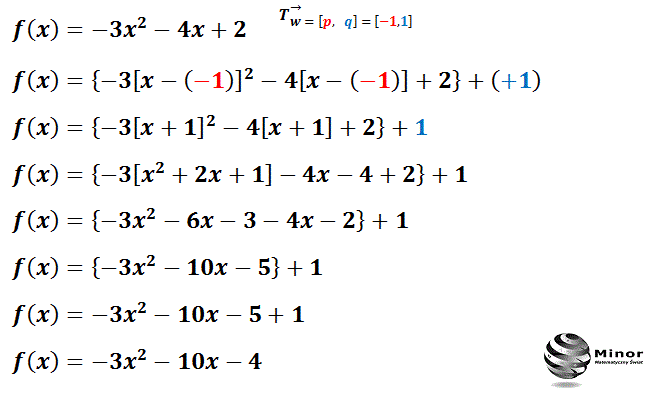



Blog Matematyczny Minor Matematyka Translacja Przesuniecia Wykresu Funkcji O Wektor




Zlaczka Pompy Shu Elbow 1 2 F X 1 2 M Aura Szczecin Pl
Steps for Solving Linear Equation f ( x ) = 1 \frac { 2 } { x 1 } , s f ( x) = 1 − x 1 2 , s Multiply both sides of the equation by x1 Multiply both sides of the equation by x 1 fx\left (x1\right)=x12 f x ( x 1) = x 1 − 2 Use the distributive property to multiply fx by x1It is very important to recognize that though the function f (x)=(1¡x)¡1 is de &ned for all x 6= 1;Given f (x) = x 2 2x – 1, find f (2) To evaluate f (x) at x = 2, I'll plug 2 in for every instance of x in the function's rule f (2) = (2) 2 2(2) – 1 To keep things straight in my head (and clear in my working), I've put parentheses around every instance of the argument 2 in the formula for f Now I



Graph Transformations



Zadania Przygotowawcze Do Egzaminu Maturalnego Z Matematyki Pdf Free Download
The maximum occurs where the denominator x^2 2 is at a mininum Clearly, x^2 2 must have a minimum of 2, because x^2 is either 0 or positive So the maximum value of f(x) is 1/2, and occurs at x = 0 On the other hand, there is no minimum, bec12 Examples of the Riemann integral 5 Next, we consider some examples of bounded functions on compact intervals Example 15 The constant function f(x) = 1 on 0,1 is Riemann integrable, and




Ex 6 5 1 I Find The Maximum And Minimum Values If Any For F X




How To Tell If A Function Is Even Or Odd 8 Steps With Pictures




Zlaczka Redukcyjna Redukcja 3 8 M Sae X 1 2 F Sae Inter Instal



Search Q Parent Functions Tbm Isch




Show That The Function F R To R Defined By F X X X2 1 For All X Belongs To R Is Neither One One Nor Onto Also If G R To




Find The Derivative Of The Following Functions From First Principle X 1 X 2 Mathematics Shaalaa Com




If F X Be Defined On 2 2 And Is Given By F X 1 2 X 0 X 1 0 X 2 And G X F X F X Find G X




Naszkicuj Wykres Funkcji F X Frac X 3 X 1 X 3 4x 2 X 6 Zadania Info Rozwiazanie Zadania Z Kwadratowa
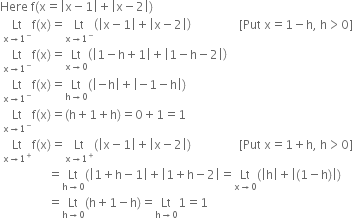



Discuss Continuity Of The Function F Given By F X X 1 X 2 At X 1 And X 2 From Mathematics Continuity And Differentiability Class 12 Cbse




Redukcja Brass M F 1 8 X 1 2




Valve For Disposable Cylinders R32 1 2 Acme F X 1 4 Sae M
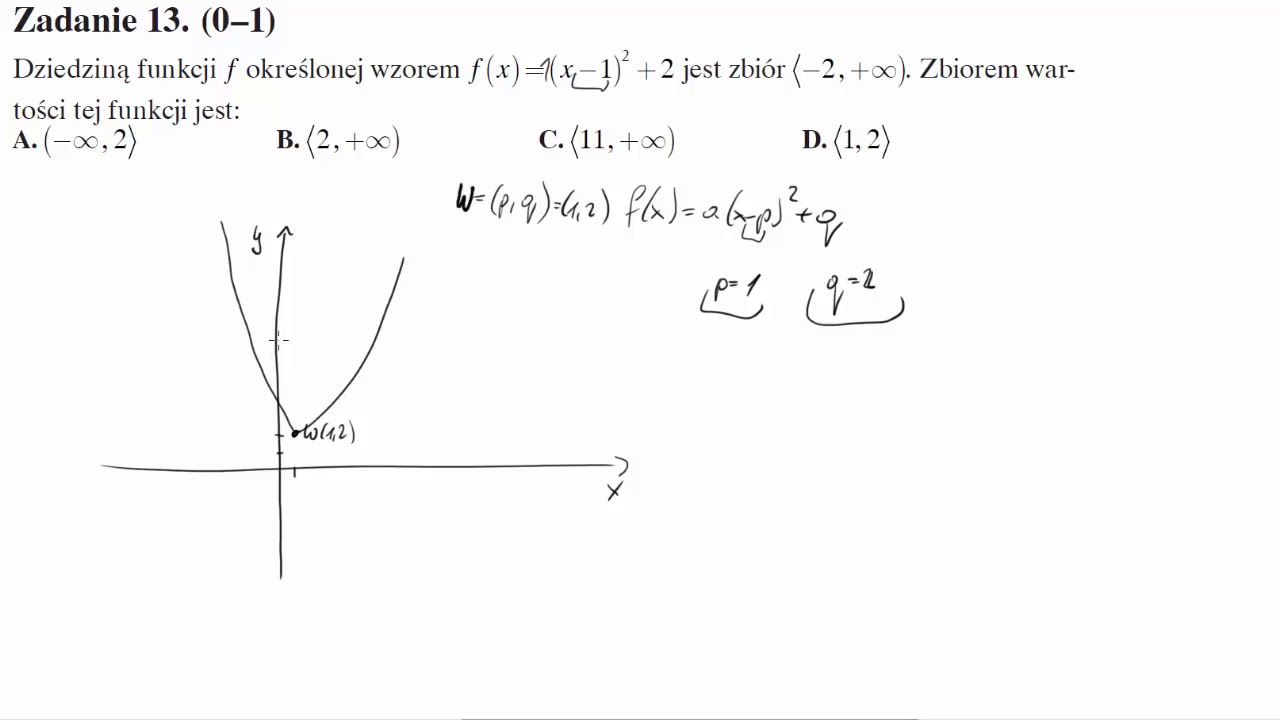



Dziedzina Funkcji F Okreslonej Wzorem F X X 1 2 2 Jest Zbior 2 Zbiorem Wartosci Tej Funkcji Jest



If F X 1 X 2 3x 2 Then What Is The Value Of F X Quora



Find The Intervals In Which The Function F X X 1 3 X 2 2 Is Sarthaks Econnect Largest Online Education Community




Redukcja 3 4 F X 1 2 M Yato Yt Toya24 Pl



Page 21 Matematyka Podrecznik Zakres Podstawowy I Rozszerzony Klasa 2
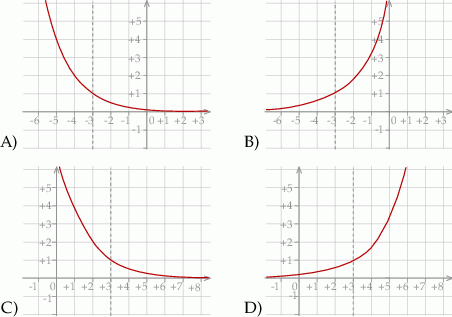



Wykres Funkcji F X Frac 1 2 X 3 Przedstawiony Jest Na Zadania Info Rozwiazanie Zadania Rozne




Miejsca Zerowe Funkcji Metoda Newtona



Yato Yt Redukcja Udarowa 3 4 F X 1 2 M Za 26 25 Zl Z Zabrzeg Allegro Pl



Http Prac Im Pwr Wroc Pl Agniesz Analiza Matematyczna Files Am Przyklady 6 Badanie Funkcji Pdf



Http Pg Gda Pl Static Mathematics Teaching Materials Calculus C E Functionsoftwovariables1 Pdf




Narysuj Wykres Funkcji F X 1 2 X 4 Podaj Jej Miesjce Zerowe



Examine The Continuity Of The Function F X X3 2x2 1 At X 1 Studyrankersonline



Mat Ug Edu Pl Rlutowsk Pub Geog Zadania Pdf
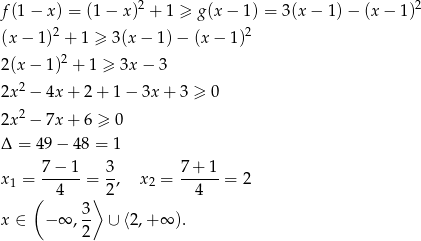



Dane Sa Funkcje F X X 2 1 I G X 3x X 2 Rozwiaz Nierownosc Zadania Info Rozwiazanie Zadania Rozwiaz Nierownosc




Narysuj Wykres Funkcji F X X 2 1 F X X 1 X 2 Najpierw Trzeba Obliczyc Wspolrzedne Brainly Pl



Nbednarz V Prz Edu Pl Download Hadewclblvdahvzg09plsjnvapjsusowcccs8sxqexehtzyrbwq0aiwa 5ddc9nx2zntjrlk2bkbwfvihmwlulrm3p6dfe Csypohmjaq Mt Di Cwiczenia 3 C2 Pdf
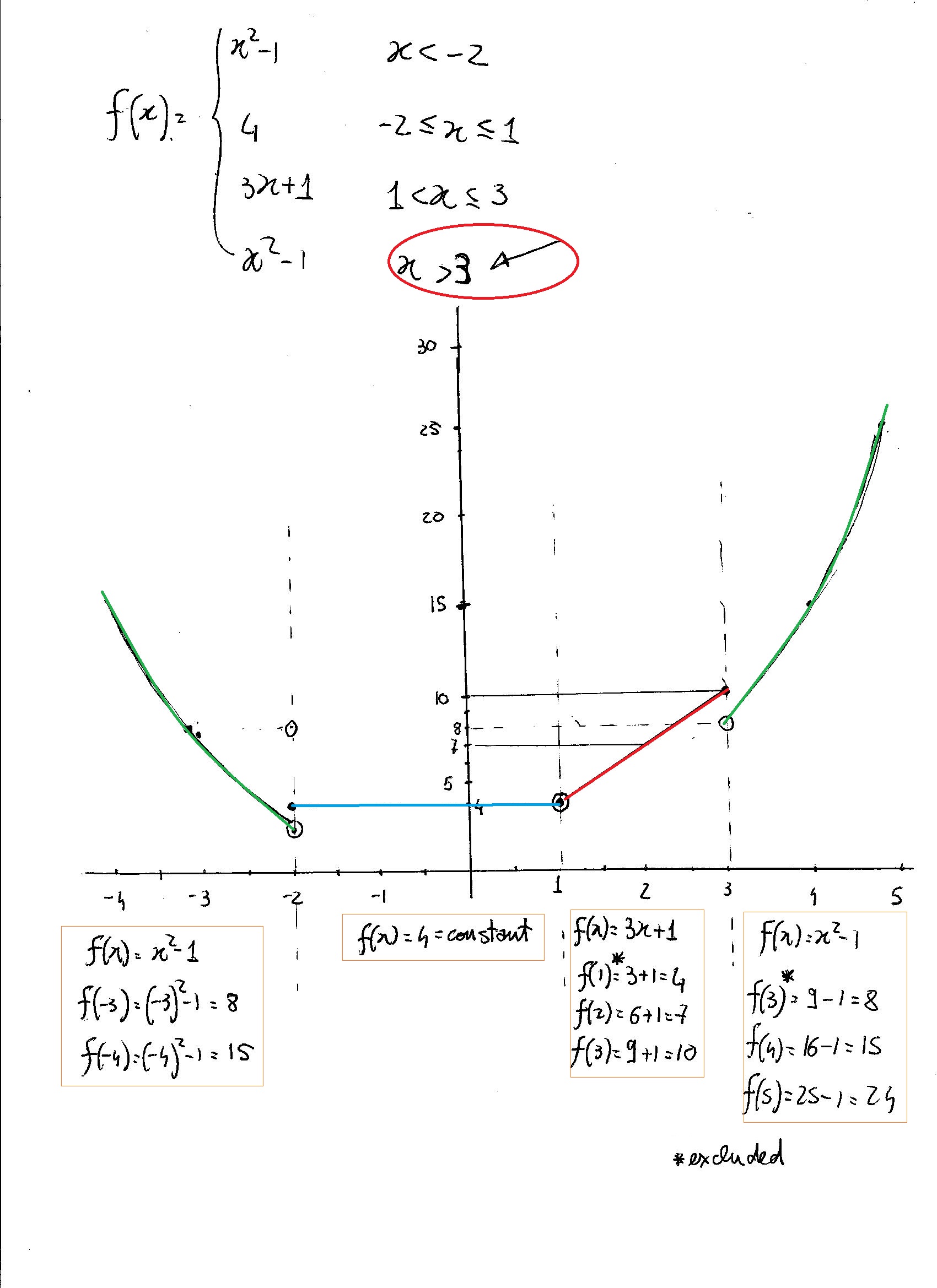



How Would You Graph F X If F X X 2 1 X 2 4 2 X 1 3x 1 1 X 3 X 2 1 X 1 How Would You Evaluate The Function At The Indicated Points F 3 F 2 F 5 F 3 Socratic
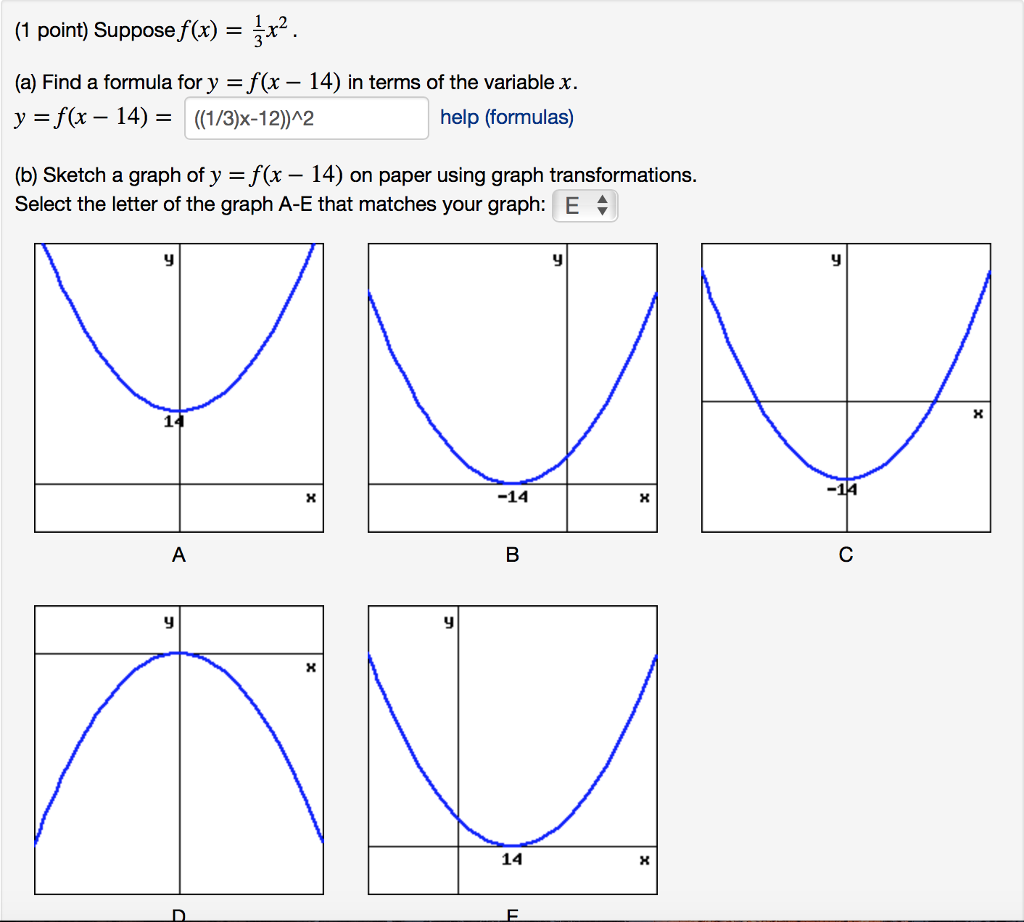



Suppose F X 1 3 X 2 A Find A Formula For Y Chegg Com




Naszkicuj Wykres Funkcji F X 2x Zadanie 2 Matematyka 1 Zakres Podstawowy Po Gimnazjum Strona 161




If F X 1 2x 1 X 1 2 Then Show That F F X 2x 1 2x 3 Provided That X 3 2dot



Nierownosci Kwadratowe




Akcesoria Do Hydrauliki Gebo Obejma Trojnika Anb 1 X 1 2 70 Mm 3 8 Mm Opinie I Ceny Na Ceneo Pl



Solution Hello How Do I Graph F X X 2 1 X 1 What Does Lim X Gt 1 X 2 1 X 1 Equal I Graphed The Function With A Discontinuity At X 1 But I 39 M Not Sure How My Second Questio



Naszkicuj Wykres Funkcji F X X 1 2




Redukcja Udarowa 3 4 F X 1 2 M Hb640 Honiton Kategorie Narzedzia Reczne Przedluzki Redukcje Przeguby Udarowe Producenci Honiton Producent I Dystrybutor Narzedzi I Wyposazenia Warsztatow Techwar




For Each Function Evaluate F 0 F 1 2 And F 2 Ppt Video Online Download
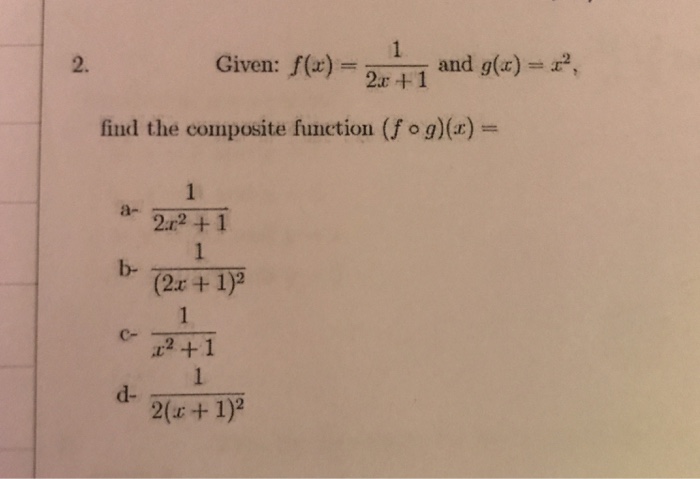



Given F X 1 2x 1 And G X X 2 Find The Chegg Com



Http Stefbar Home Amu Edu Pl Students So2 Pdf




For Which Of The Following Functions F Is F X F 1 X For All X Gmat Tutor In Nyc Online




Funkcja Kwadratowa F Jest Okreslona Wzorem F X A X 1 X 3 Wspolczynnik A We Wzorze Funkcji Zadania
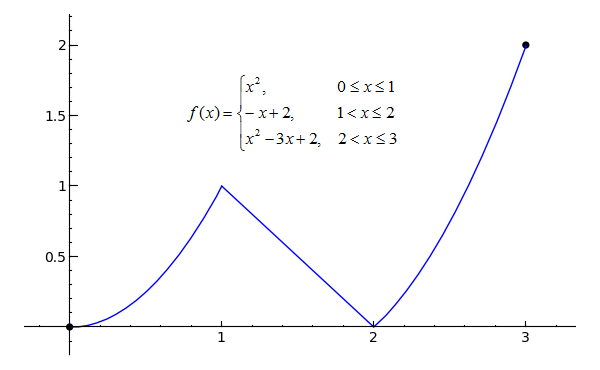



Sage Calculus Tutorial Continuity
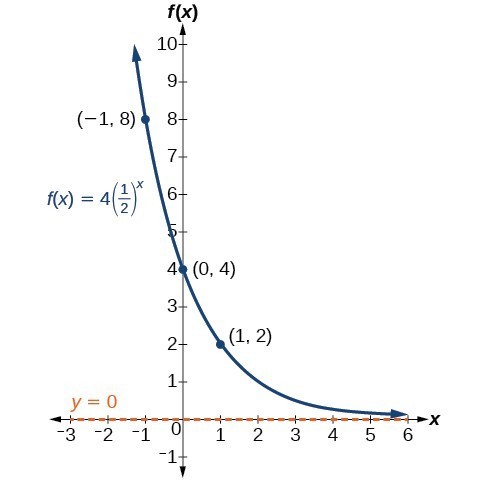



Stretching Compressing Or Reflecting An Exponential Function College Algebra




Najti F 1 2 F X X 1 X 2 3 F X 2x 1 2x 1 4 F X 2x 1 7x5 F X 2x 3 5 4x Shkolnye Znaniya Com



Przebieg Zmiennosci I Wykres F X X 1 X 2
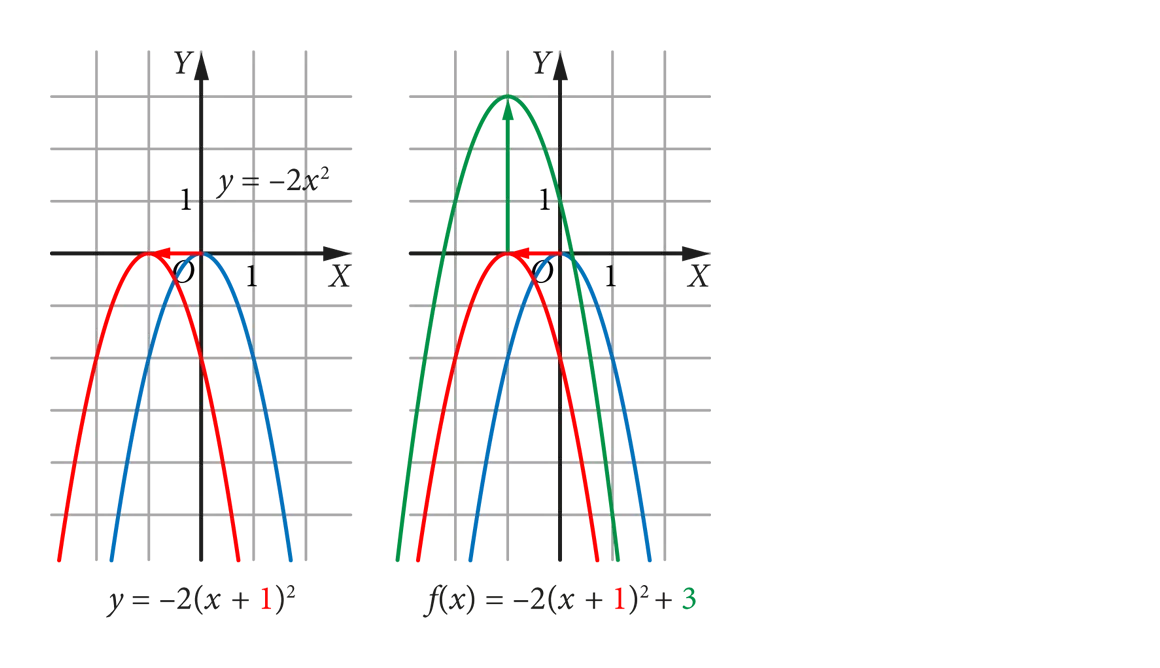



Postac Kanoniczna Funkcji Kwadratowej F X A X P 2 Q Dlaucznia Pl




Dany Jest Wykres Funkcji Y F X Narysuj Wykres Funkcji H X F X 2 Youtube
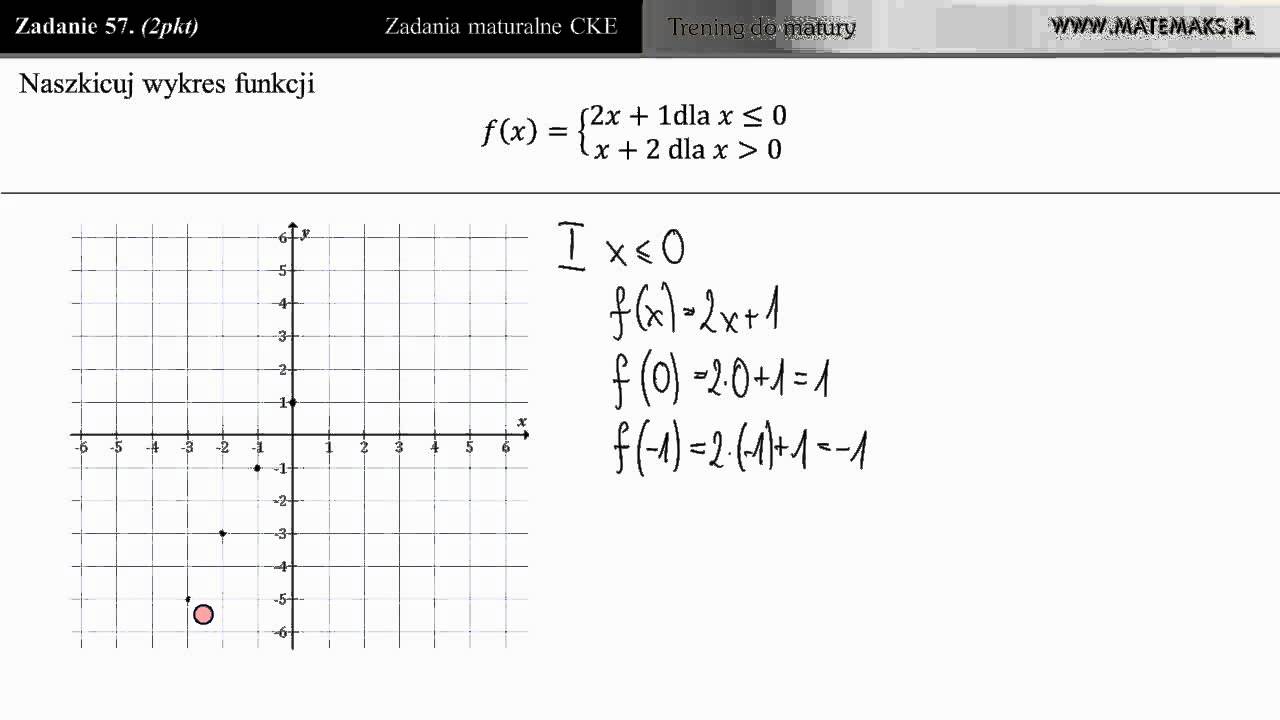



Zad 57 Naszkicuj Wykres Funkcji Trening Do Matury Youtube




Dedra
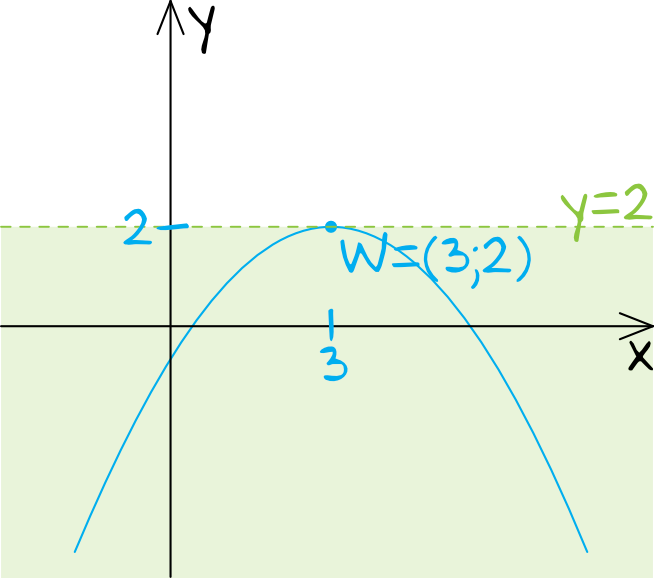



Wykres Funkcji F X 1 2 X 3 2 2 Ma Dwa Punkty Wspolne Z Prosta O Rownaniu Y M Jezeli Zadania
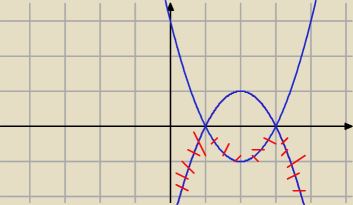



Wykres




If The Function F X X 2 1 X 1 When X 1 K When X 1




Redukcja 3 4 F X 1 2 M Udarowa Hitachi Adaptery Przejsciowki Narzedziownia Shop



Naszkicuj Wykres Funkcji F X 2x A Nastepnie Stosujac Odpowiednie Zaliczaj Pl



2



F X X 2 Graph



Naszkicuj Wykres Funkcji F X 1 2 X I Omow Jej Wlasnosci Matematyka Pracadomowa24 Pl




14 Grafica De Las Funciones F X 1 E X F X 1 2 X Download Scientific Diagram



Wykresem Funkcji F X X2 Bx C Jest Parabola O Wierzcholku W Punkcie W Wyznacz Zaliczaj Pl




Naszkicuj Wykres Funkcji F X 1 X Zadanie 1 Matematyka 2 Zakres Podstawowy Po Gimnazjum Strona 46



Biomath Transformation Of Graphs
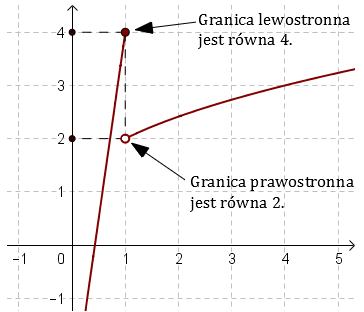



Granice Jednostronne Funkcji




Ex 1 2 1 Class 12 Maths Show F X 1 X Is One One Onto Where R




Dana Jest Funkcja F Okreslona Wzorem F X X 1 2 2 Naszkicuj Wykres Funkcji F A Nastepnie Naszkicuj Brainly Pl




If F X 2x 1 If X Gt 1 And X 2 1 If 1 Lt X Lt 1 And If F 1 F 3 F X F 2 F Youtube
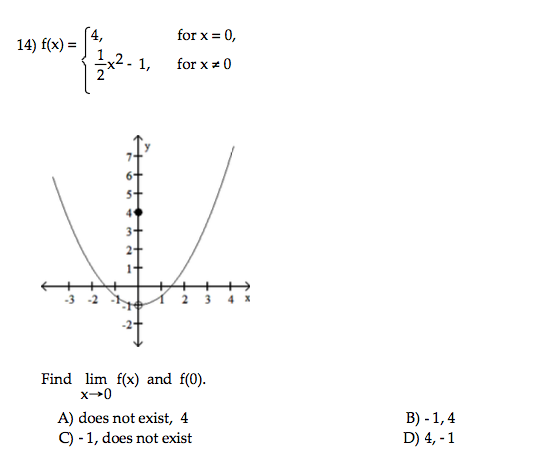



F X 4 For X 0 1 2 X 2 1 For X Notequalto 0 Chegg Com




If F X X 1 4 X 2 3 X 3 2 X 4 Then The Value Of F 1 F 2 F 3 F 4 Equals




Naszkicuj Wykres Funkcji F X 4 X Zadanie 1 Matematyka 2 Zakres Podstawowy Po Gimnazjum Strona 44



Let F X Max 2x 1 3 4x Where X Is Any Real Number Then The Minimum Possible Value Of F X Is Quora



Sporzadz Wykres Funkcji F X 3x 1 X 1 Matematyka Pracadomowa24 Pl



F X 1 X




Maximum Value Of Function F X Frac X 4 X 2 X 6 2x 3 1 When X 1 Mathematics Stack Exchange



Wykres Funkcji F X A B Matematyka Matura




Redukcja Udarowa 3 4 F X 1 M Yato Yt 1168 Toya24 Pl



Find F 1 If F X X 1 2x 2 7x 5 When X 1 F X 1 3 When X 1 Sarthaks Econnect Largest Online Education Community




Adapter Do Nasadek Udarowych 3 4 F X 1 2 M Crmo Warynski



0 件のコメント:
コメントを投稿